How deep can we drill with steel drill rods?

By Colin Rice

What is the link between Yield Strength and depth rating? Find out more about this very interesting relationship here.

This is the first article of Part 2 of our Technical Series on Drill Rod Safety. Click here for an outline of the entire Technical Series on Drill Rod Safety.

In Part 1 of the Drill Rod Safety Series, we discussed how seamless steel tubing is manufactured and we discussed some important mechanical properties. Building on this knowledge, this article highlights the important relationship between yield strength and the depth limitations of drill rods.

A very INTERESTING AND important relationship!

All wireline drill rod manufacturers specify the depths to which their drill rods can be used and they typically quote lesser depth capability as the diameter of the drill rod increases. This is not logical!

There are many factors that determine how deep one can safely drill with a given drillstring and this article will discuss some of these factors. 

Firstly, an interesting relationship will be derived that will answer an extremely important question – “how deep can we drill with a steel drill rod”? The result will probably surprise many people!

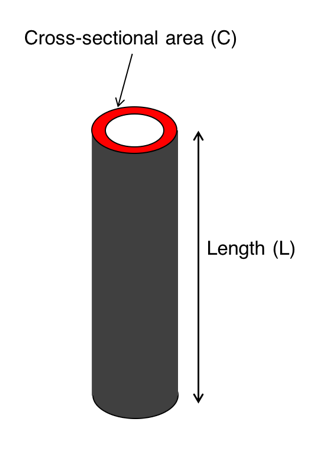
From the first article in this series, we know that: 

$$stress = {force \over cross\,sectional\,area}$$

Using this relationship, we can determine the stress at any point in the drillstring. Let's assume that we have a drillstring of length L metres hanging freely in a straight vertical borehole. Now, let's calculate the stress at the top most joint:

Assume:

$$density\,of\,steel = s\,kg\,per\,litre$$ $$length\,of\,drillstring = L\,metres$$ $$cross\,sectional\,area\,of\,drill\,rod = C$$

Then we can say:

$$mass\,of\,the\,drillstring = {L \times C \times s \over 1000}kg$$

 And,

$$weight\,of\,the\,drillstring = {L \times C \times s \times g \over 1000}N$$

And therefore,

$$stress\,at\,the\,topmost\,joint = {L \times C \times s \times g \over 1000 \times C}N$$

If we assume that the density of steel is 7,85 kilograms per litre, then we can say that:

$$stress\,at\,the\,topmost\,joint = {L \times C \times 7,85 \times g \over 1000 \times C}N$$

and so, by simplifying the relationship we can say:

$$stress\,at\,the\,topmost\,joint = 0,077 \times L$$

This is an incredibly interesting result! It tells us that the stress at any point in a drillstring is a function only of the length of the drillstring hanging below the point - it is independent of the dimension of the drill rod being used. This is surprising and this is incredibly important!

Let us assume that we have a drillstring of 1000 metres hanging freely in a vertical borehole – the stress in the top-most drill rod will be 77 MPa irrespective of the size of the drill rod, AQ, BQ, PQ or even 1 000 mm diameter!

Now that we have established this relationship, we can very easily determine the greatest depth to which we can drill with any given drillstring.

Let us assume that our drill rod is manufactured from SAE 1541 material (Yield Strength = 620 MPa and UTS = 700 MPa).

If we substitute 700 MPa into the relationship that we developed above and determine “L” then we can determine the depth at which the drillstring will fail under its own weight:

The calculation is as follows:

$$700 = 0,077 \times L$$ $$L = {700 \over 0,077}$$ $$L = 9100\,metres$$

So, we can now say that a drillstring manufactured from SAE 1541 material will fail under its own weight at 9 100 metres and so by extension, we can say that the deepest borehole that we can drill with this material would be 9 100 metres. If we want to drill deeper boreholes then we need material with a greater ultimate tensile strength (UTS).

From a practical point of view, we should use 620 MPa, the Yield Strength in determining L rather than 700 MPa, the UTS - we cannot use drill rods that are permanently stretched.

If we use 620 MPa rather than 700 MPa, then we will find that L = 8 000 metres (approximately) and so we can say that at 8 000 metres the top most drill rod will “yield”, ie. it will permanently stretch. The maximum practical depth limit of our drillstring is therefore 8 000 metres.

Of course, this would not be advisable: it would be very foolish to use a drillstring to its ultimate limit. It is standard engineering practice to apply a factor of safety to our calculation so let’s now be a bit more practical - let’s apply a factor of safety of 2 to our calculation – on this basis, the deepest that we can “safely” drill is now 8 000 divided by 2 = 4 000 metres.

But, this is not possible - unfortunately, it is not possible to purchase a single length of material that is 4 000 metres long – we have to purchase shorter lengths and then cut a pin and a box thread into the tube so that we can join the drill rods together.

It should be clear that to cut a pin or a box thread into the tube, it is necessary to remove at least half the wall thickness from each end and so, because we have removed half of the wall thickness we have halved the cross-sectional area and so we have effectively doubled the stress at the connection. The effect of this is that the threaded connections further reduce the maximum depth to which we can “safely” drill again by a factor of at least 2.

We can now say that the maximum depth to which we can safely drill with drill rod manufactured from SAE 1541 material is 4 000 divided by 2 = 2 000 metres.

Obviously, if we used material with a higher Yield Strength then we could safely drill even deeper boreholes.

It is very important to recognise that this maximum depth is independent of the dimensions of the drill rod – in theory, we could drill to       2 000 metres with A, B or N size drill rods. In effect this is not strictly true because of issues around the design of the threads (the thread efficiency).

In the next article in this series, we look at thread design and the concept of thread efficiency. 

---

Other articles in part 2 of the drill rod Series.